Exponential Growth

In exponential growth, the population’s growth rate increases over time, in proportion to the size of the population. As an example for exponential growth, we will use bacteria grown in labs. Unlike logistic growth, it is not limited by a maximum limit or carrying capacity.

Bacteria reproduce by binary fission (splitting in half), and the time between divisions is about an hour for many bacterial species. To see this exponential growth, let’s start by placing 1000 bacteria in a flask with an unlimited supply of nutrients.

• After 1 hour, each bacterium will divide, yielding 2000 bacteria (an increase of 1000$bacteria).
• After 2 hours, each of the 2000 bacteria will divide, producing 4000 (an increase of 2000 bacteria).
• After 3 hours, each of the 4000 bacteria will divide, producing 8000 (an increase of 4000 bacteria).

The key concept of exponential growth is that the population growth rate—the number of organisms added in each generation—increases as the population gets larger. And the result can be dramatic: after 1 day (24 cycles of division), our bacterial population would have grown from 1000 to over 16 billion. When population size, $N$, is plotted over time, a J-shaped growth curve is made.

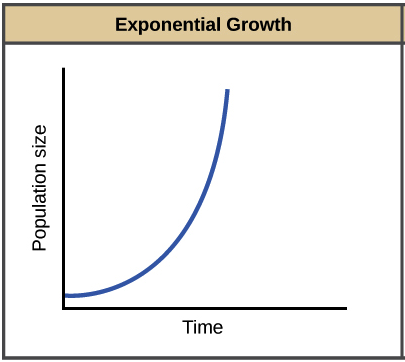
The result is an exponential growth when $r$ (the per capita rate of increase) for the population is positive and constant. While any positive, constant $r$ can lead to an exponential growth, you will often see exponential growth represented with an $r$ of $r_{max}$.

$r_{max}$ is the maximum per capita rate of increase for a particular species under ideal conditions, and it varies from species to species. For instance, bacteria can reproduce much faster than humans, and would have a higher maximum per capita rate of increase. The maximum population growth rate for a species, sometimes called its biotic potential, is expressed in the following equation:

$\frac{dN}{dT}=r_{max}N$