Solving Linear Equations and Linear Inequalities

How do I Solve Linear Equations?

Equivalence

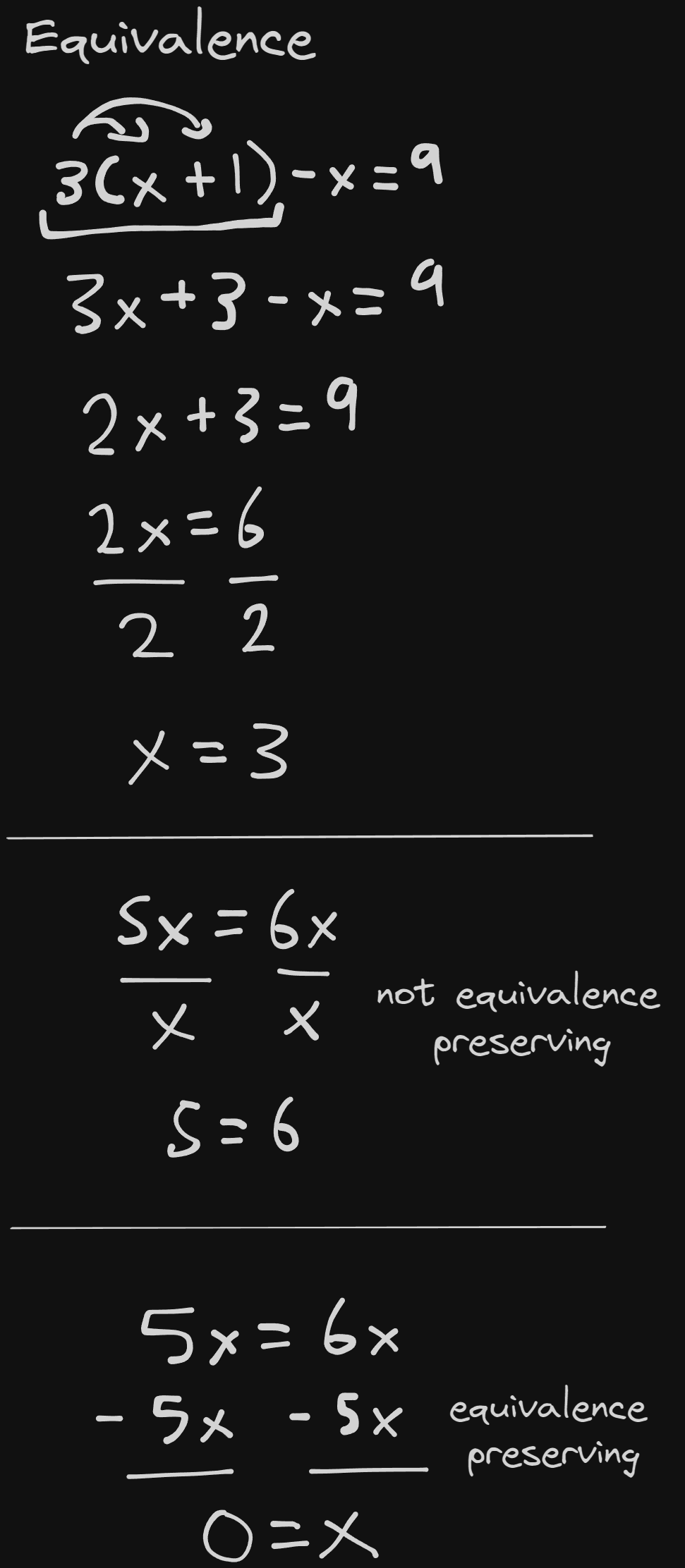
Types of Linear Equations

The goal of solving a linear equation is to find the value of a variable; we isolate the variable step by step until only the variable is on one side of the equation and only a constant is on the other.

When solving linear equations, the most important thing to remember is that the equation will remain equivalent to the original equation only if we always treat both sides equally: whenever we do something to one side, we must do the exact same thing to the other side.

Linear Equations in One Variable

Most of these questions on the SAT contain only one variable.

Example: If $2x+1=5$, what is the value of $x$?

Answer:

x = 2

Linear Equations in Two Variables

Sometimes, we’re given an equation in two variables and we’re told the value of one of the variables. Plug the value of the known variable into the equation and solve.

Example: If $2x+5y=1$ and $x=3$, what is the value of $y$?

Answer:

y = -1

---

How do I alter the number of solutions for linear equations?

Note: Questions about the number of solutions for linear equations do not appear on every test.

Creating an equation with no solutions

$-11x+4=-11x+-11$

Added $11x$ to both sides to cancel each other out, resulting in $4=-11$, thus creating no solutions.

Creating an equation with infinitely many solutions

$4(x-2)+x=5x+$ $4x-8+x=5x+(-8)$ $5x-8=-5x-8$ $-8=-8$

How many solutions can a linear equation have?

Most linear equations on the SAT have exactly one solution. Linear equations with no solutions or infinitely many solutions must be engineered by specifying the values of constants.

For a linear equation in one variable:

• If the equation can be rewritten in the form $x=a$, where $a$ is a constant, then that equation has one variable.
• If the variable can be eliminated from the equation, and what remains is the equation $a=b$, where $a$ and $b$ are different constants, then the equation has no solution. (No value of $x$ can make $1$ equal to $2$.)
• If the equation can be rewritten in the form $x=x$, then the solution has infinitely many solutions. (No matter what the value of $x$ is, it will always equal itself!)

Example: $2x-1=ax-2$

If $a=2$ in the equation above, what value of $x$ satisfies the equation?

Answer:

No value of x satisfies the equation.

Example: $3ax-11=4(x+2)+2(x-1)$

If the equation above, $a$ is a constant. If no value of $x$ satisfies the equation, what is the value of $a$?

Answer:

Steps:
1. Distribute and combine the like terms on the right side of the equation.
2. Solve 3ax = 6x for a to create and impossible equation.
 
a = 2

Things to Remember

When solving linear equations, the most important thing to remember is that the equation will remain equivalent to the original equation only if we always treat both sides equally: whenever we do something to one side, we must do the exact same thing to the other side.

When solving linear inequalities:

• If the coefficient of $x$ is positive, the inequality sign maintains its direction when we divide by the coefficient to isolate $x$.
• If the coefficient of $x$ is negative, we must reverse the direction of the inequality sign when we divide by the coefficient to isolate $x$.

When determining the number of solutions for a linear equation:

• If the equation can be rewritten in the form $x=a$, where $a$ is a constant, then that equation has one variable.
• If the variable can be eliminated from the equation, and what remains is the equation $a=b$, where $a$ and $b$ are different constants, then the equation has no solution. (No value of $x$ can make $1$ equal to $2$.)
• If the equation can be rewritten in the form $x=x$, then the solution has infinitely many solutions. (No matter what the value of $x$ is, it will always equal itself!)