Understanding Linear Relationships

What are Linear Relationships?

A linear relationship is any relationship between two variables that creates a line when graphed in the $xy$-plane.

Linear Relationships

Linear equations can be used to represent the relationship between two variables, most commonly $x$ and $y$. To form the simplest linear relationship, we can make our two variables equal:

$y=x$

By plugging numbers into the equation, we can find some relative values of $x$ and $y$.

$x$	$y$
0	0
1	1
2	2
3	3
If we plot these points in the $xy$-graph, we create a line.

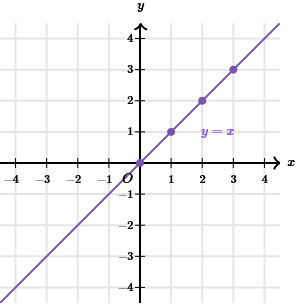
Every possible linear relationship is just a modification of this simple equation. We might multiply one of the variables by a coefficient or add a constant to one side of the equation, but we’ll still be creating a linear relationship.

How do we translate word problems into linear equations?

Modeling Real World Scenarios

Translating Word Problems

It may not be hard to translate “Maya is $3$ inches taller than Geoff” into a linear equation, but some SAT word problems are several sentences long, and the information we need to build an equation may be scattered around.

Examples

A car with a price of $17,000$ is to be purchased with an initial payment of $5,000$ and monthly payments of $240$. Which of the following equations can be used to find the number of monthly payments, $m$, requires to complete the purchase, assuming there are no taxes or fees.

Translation:

We're given three important values here: 17,000, 5,000, and 240.
- $17,000 is the total price, so that's what everything else needs to add up to.
- $5,000 is a one-time payment.
- $24 is a constant amount that's paid every month, so it needs to be multipled by m, the number of months.
‎ 
The total price, $17,000, euqals the sum of the other payments: the inital $5,000 payment and the $240 paid each month (m).
‎ 
17,000 = 5,000 + 240m

What will we be asked to do in linear equations word problems?

On the test, we may be asked to:

• Write our own equation based on the word problem
• Write our own equation and then solve it
• Solve a given equation based on the word problem

Example

A helicopter, initially hovering $35$ feet above the ground, begins to ascend at a speed of $16$ feet per second. Write an equation that can be used to find $t$, the number of seconds it takes for the helicopter to reach $179$ feet above the ground.

The total height, which everything else must add up to, is $179$ feet.

The starting height of the helicopter is $35$ feet.

The amount of time it takes is $t$ seconds.

We can write the equation as $179=35+16t$

Linear Functions

Any linear equation with two variables is technically a function. Linear functions are usually written in either slope-intercept form or standard form. We need a thorough and flexible understanding of these forms in order to approach many SAT questions about linear relationships.

Slope-intercept Form

The slope-intercept form of a linear function, $y=mx+b$, where $m$ and $b$ are constants, tells us both the slope and the $y$-intercept of the line:

• The slope is equal to $m$.
• The $y$-intercept is equal to $b$.

Standard Form

The standard form of a linear function, $Ay+Bx=C$, where, $A$, $B$, and $C$ are constants, will always be used in word problem scenarios that have two outputs, instead of an input and an output. To find the slope or $y$-intercept of a line in standard form, it’s often convenient to convert the equation to slope-intercept form by isolating $y$.

What will we be asked to do in linear function word problems?

On the test, we may be asked to:

• Write our own linear function based on the word problem (We may need to calculate the slope or  $y$-intercept in more challenging questions.)
• Identify the meaning of a value in a given function that models a scenario

Things to Remember

$slope=\frac{y_2-y_1}{x_2-x_1}$ The slope-intercept form of a linear equation, $y=mx+b$, tells us both the slope and the $y$-intercept of the line:

• The slope is equal to $m$.
• The $y$-intercept is equal to $b$.

We can write the equation of a line as long as we know either of the following:

• The slope of the line and a point on the line
• Two points on the line